為了要讓 QSP 可以作用在更高維度的希爾伯特空間 (更多 qubit)，我們需要一些工具，其中之一就是今天要介紹的 block-encoding。

還記得昨天 QSP 的介紹中，我們多項式轉換的目標是一實數 ，而 signal rotation operator 把 「」這個資訊「編碼」(encode) 在他的左上角：

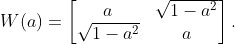
若將實數推廣到矩陣：令 為任意 的矩陣，若大小 的么正矩陣 滿足

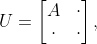
則我們說「 block-encodes 」("" 是 矩陣)。Block-encoding 能以更普遍的形式表示，如 可以是 的矩陣， 不必在左上角等等；不過為了保持簡潔，我們暫時不需要！另外，雖然說 是「任意」矩陣，但為了滿足 的么正性質， 是必要的。順帶一提，

Block-encoding 是個應用廣泛的概念，除了 QSP 之外，還可應用在前幾天提到的 oblivious AA：假設 是某一僅有一份、未知的量子態，且讓 和 做 tensor product 形成 ；而我們感興趣的量子態是 ( 不一定有規一化 (normalized)，因為 不一定是 unitary)。若 block-encodes ，則

簡而言之，只要 是 的 block-encoding，我們就能透過 對 做 oblivious AA！(若循著 block-encoding 的思路，在 [AA] Oblivious AA 那篇所提出的三個問題也就能解決了！)